原创文章，转载请务必将下面这段话置于文章开头处。
本文转发自技术世界，原文链接 http://www.jasongj.com/ml/associationrules/

关联规则背景

关联规则来源

上个世纪，美国连锁超市活尔玛通过大量的数据分析发现了一个非常有趣的现象：尿布与啤酒这两种看起来风马牛不相及的商品销售数据曲线非常相似，并且尿布与啤酒经常被同时购买，也即购买尿布的顾客一般也同时购买了啤酒。于是超市将尿布与啤酒摆在一起，这一举措使得尿布和啤酒的销量大幅增加。

原来，美国的妇女通常全职在家照顾孩子，并且她们经常会嘱咐丈夫在下班回家的路上为孩子买尿布，而丈夫在买尿布的同时又会顺手购买自己爱喝的啤酒。

注：此案例很精典，切勿盲目模仿案例本身，而应了解其背后原理。它发生在美国，而且是上个世纪，有些东西并不一定适用于现在，更不一定适用于中国。目前国内网购非常普遍，并不一定需要去超市线下购买，而网购主力军是女性，因此不一定会出现尿布与啤酒同时购买的问题。另外，对于线下销售，很多超市流行的做法不是把经常同时购买的商品放在一起，而是尽量分开放到不同的地方，这样顾客为了同时购买不得不穿过其它商品展示区，从而可能购买原来未打算购买的商品。

但是本案例中背后的机器学习算法——关联规则，仍然适用于非常多的场景。目前很多电商网站也会根据类似的关联规则给用户进行推荐，如比较常见的“购买该商品的客户还购买过**”。其背后的逻辑在于，某两种或几种商品经常被一起购买，它们中间可能存在某种联系，当某位顾客购买了其中一种商品时，他/她可能也需要另外一种或几种商品，因此电商网站会将这几种商吕推荐给客户。

什么是关联规则

如同上述啤酒与尿布的故事所示，关联规则是指从一组数据中发现数据项之间的隐藏关系，它是一种典型的无监督学习。

关联规则的核心概念

本节以上述超市购物的场景为例，介绍关联规则的几个核心概念

项目
一系列事件中的一个事件。对于超市购物而言，即一次购物中的一件商品，如啤酒

事务
一起发生的一系列事件。在超市购物场景中，即一次购买行为中包含的所有商品的集合。如 $\{尿布，啤酒，牛奶，面包\}$

项集
一个事务中包含的若干个项目的集合，如 $\{尿布，啤酒\}$

支持度
项集 $\{A，B\}$ 在全部项集中出现的概率。支持度越高，说明规则 $A \rightarrow B$ 越具代表性。

频繁项集
某个项集的支持度大于设定的阈值（人为根据数据分布和经验设定），该项集即为频繁项集。

假设超市某段时间总共有 5 笔交易。下面数据中，数字代表交易编号，字母代表项目，每行代表一个交易对应的项目集

1: A B C D
2: A B
3: C B
4: A D
5: A B D

对于项集 $\{A，B\}$，其支持度为 $3/5=60\%$ （总共 5 个项集，而包含 $\{A，B\}$ 的有 3 个）。如果阈值为 $50\%$，此时 $\{A，B\}$ 即为频繁项集。

置信度
在先决条件 $A$ 发生的条件下，由关联规则 $A \rightarrow B$ 推出 $B$ 的概率，即在 $A$ 发生时，$B$ 也发生的概率，即 $P(A|B)$ 。置信度越高，说明该规则越可靠。

在上例中，频繁项集 $\{A，B\}$ 的置信度为 $3/4=75\%$ （包含 $\{A，B\}$ 的项集数为 3，包含 $A$ 的项集数为 5）

满足最小支持度和最小置信度的规则，即为强关联规则。

提升度
$A$ 发生时 $B$ 也发生的概率，除以 $B$ 发生的概率，即 $P(A|B) / P(B)$ ，它衡量了规则的有效性。

在上例中，置信度为 $75\%$ ，但是否能说明 $A$ 与 $B$ 之间具有强关联性呢？提升度为 $75\% / 80\% = 93.75\%$

从中可以看出，$B$ 的购买率为 $80\%$，而购买 $A$ 的用户同时购买 $B$ 的概率只有 $75\%$，所以并不能说明 $A \rightarrow B$ 是有效规则，或者说这条规则是没有价值的，因此不应该如本文开头处啤酒与尿布的案例中那样将 $A$ 与 $B$ 一起销售。

提升度是一种比较简单的判断规则是否有价值的指标。如果提升度为 1，说明二者没有任何关联；如果小于 1，说明 $A$ 与 $B$ 在一定程度上是相斥的；如果大于 1，说明 $A$ 与 $B$ 有一定关联。一般在工程实践中，当提升度大于 3 时，该规则才被认为是有价值的。

Apriori算法

关联规则中，关键
点是：1）找出频繁项集；2）合理地设置三种阈值；3）找出强关联规则

直接遍历所有的项目集，并计算其支持度、置信度和提升度，计算量太大，无法应用于工程实践。

Apriori算法可用于快速找出频繁项集。

Apriori算法原理

原理一：如果一个项集是频繁项目集，那它的非空子集也一定是频繁项目集。

原理二：如果一个项目集的非空子集不是频繁项目集，那它也不是频繁项目集。

例：如果 $\{A，B，C\}$ 的支持度为 $70\%$，大于阈值 $60\%$，则 $\{A，B，C\}$ 为频繁项目集。此时 $\{A，B\}$ 的支持度肯定大于等于 $\{A，B，C\}$ 的支持度，也大于阈值 $60\%$，即也是频繁项目集。反之，若 $\{A，B\}$ 的支持度为 $40\%$，小于阈值 $60\%$，不是频繁项目集，则 $\{A，B，C\}$ 的支持度小于等于 $40\%$，必定小于阈值 $60\%$，不是频繁项目集。

原理三：对于频繁项目集X，如果 $(X-Y) \rightarrow Y$ 是强关联规则，则 $(X-Y) \rightarrow Y_{sub}$ 也是强关联规则。

原理四：如果 $(X-Y) \rightarrow Y_{sub}$ 不是强关联规则，则 $(X-Y) \rightarrow Y$ 也不是强关联规则。

其中 $Y_{sub}$ 是 $Y$ 的子集。

这里把包含 $N$ 个项目的频繁项目集称为 $N-$ 频繁项目集。Apriori 的工作过程即是根据 $K-$ 频繁项目集生成 $(K+1)-$ 频繁项目集。

根据数据归纳法，首先要做的是找出1-频繁项目集。只需遍历所有事务集合并统计出项目集合中每个元素的支持度，然后根据阈值筛选出 $1-$ 频繁项目集即可。

Apriori生成频繁项集

有项目集合 $I=\{A，B，C，D，E\}$ ，事务集 $T$ ：

A，B，C
A，B，D
A，C，D
A，B，C，E
A，C，E
B，D，E
A，B，C，D

设定最小支持度 $support=3/7$，$confidence=5/7$

直接穷举所有可能的频繁项目集，可能的频繁项目集如下

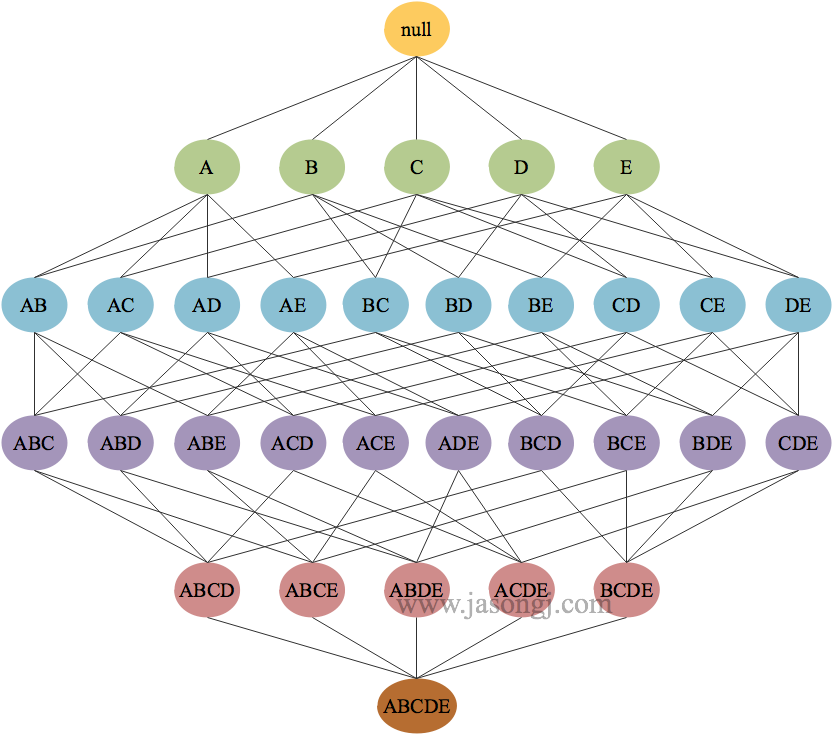
1-频繁项目集
1-频繁项目集，即

1	{A}，{B}，{C}，{D}，{E}

其支持度分别为 $6/7$，$5/7$，$5/7$，$4/7$和$3/7$，均符合支持度要求。

2-频繁项目集
任意取两个只有最后一个元素不同的 $1-$ 频繁项目集，求其并集。由于每个 $1-$ 频繁项目集只有一个元素，故生成的项目集如下：

{A，B}，{A，C}，{A，D}，{A，E}
{B，C}，{B，D}，{B，E}
{C，D}，{C，E}
{D，E}

过滤出满足最小支持度 $3/7$的项目集如下

1	{A，B}，{A，C}，{A，D}，{B，C}，{B，D}

此时可以将其它所有 $2-$ 频繁项目集以及其衍生出的 $3-$ 频繁项目集， $4-$ 频繁项目集以及 $5-$ 频繁项目集全部排除（如下图中红色十字所示），该过程即剪枝。剪枝减少了后续的候选项，极大降低了计算量从而大幅度提升了算法性能。

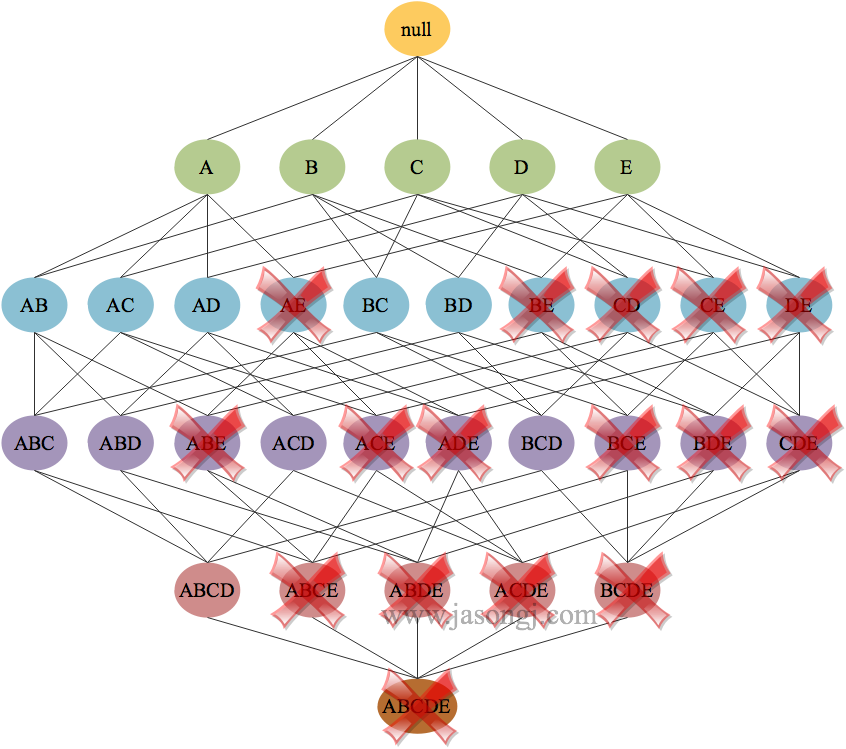
3-频繁项目集
因为 $\{A，B\}$，$\{A，C\}$，$\{A，D\}$ 除最后一个元素外都相同，故求 $\{A，B\}$ 与 $\{A，C\}$ 的并集得到 $\{A，B，C\}$，求 $\{A，C\}$ 与 $\{A，D\}$ 的并集得到 $\{A，C，D\}$，求 $\{A，B\}$ 与 $\{A，D\}$ 的并集得到 $\{A，B，D\}$。但是由于 $\{A，C，D\}$ 的子集 $\{C，D\}$ 不在 $2-$ 频繁项目集中，所以需要把 $\{A，C，D\}$ 剔除掉。$\{A，B，C\}$ 与 $\{A，B，D\}$ 的支持度分别为 $3/7$ 与 $2/7$，故根据支持度要求将 $\{A，B，D\}$ 剔除，保留 $\{A，B，C\}$。

同理，对 $\{B，C\}$ 与 $\{B，D\}$ 求并集得到 $\{B，C，D\}$，其支持度 $1/7$ 不满足要求。

因此最终得到 $3-$ 频繁项目集 $\{A，B，C\}$。

排除 $\{A，B，D\}$ ， $\{A，C，D\}$， $\{B，C，D\}$ 后，相关联的 $4-$ 频繁项目集 $\{A，B，C，D\}$ 也被排除，如下图所示。

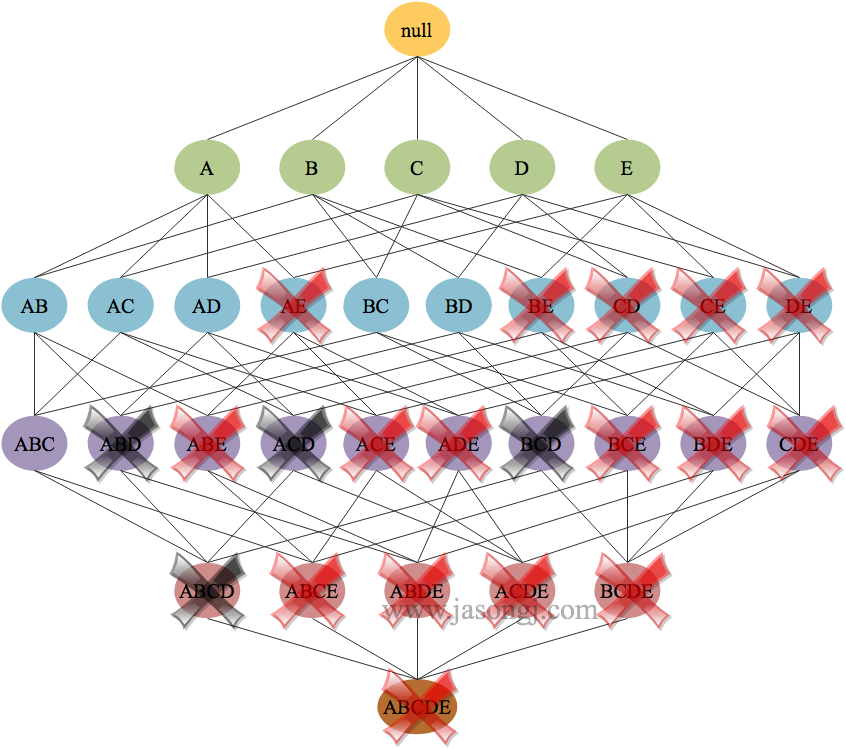
生成强关联规则

穷举法
得到频繁项目集后，可以穷举所有可能的规则，如下图所示。然后通过置信度阈值筛选出强关联规则。

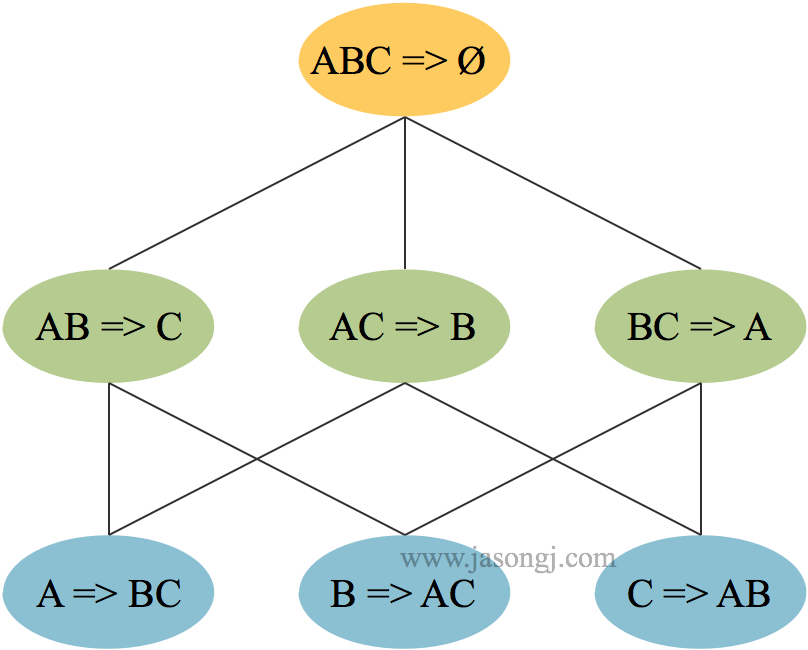
Apriori剪枝
Apriori算法可根据原理三与原理四进行剪枝，从而提升算法性能。

上述步骤得到了3-频繁项集 $\{A，B，C\}$。先生成 $1-$ 后件（即箭头后只有一个项目）的关联规则

$\{A，B\} \rightarrow C $ 置信度 $3/4 > 5/7$，是强关联规则
$\{A，C\} \rightarrow B $ 置信度为 $3/5 < 5/7$，不是强关联规则
$\{B，C\} \rightarrow A $ 置信度为 $3/3 > 5/7$，是强关联规则

此时可将 $\{A，C\} \rightarrow B $ 排除，并将相应的 $2-$ 后件关联规则 $\{A\} \rightarrow \{B，C\} $ 与 $\{C\} \rightarrow \{A，B\} $ 排除，如下图所示。

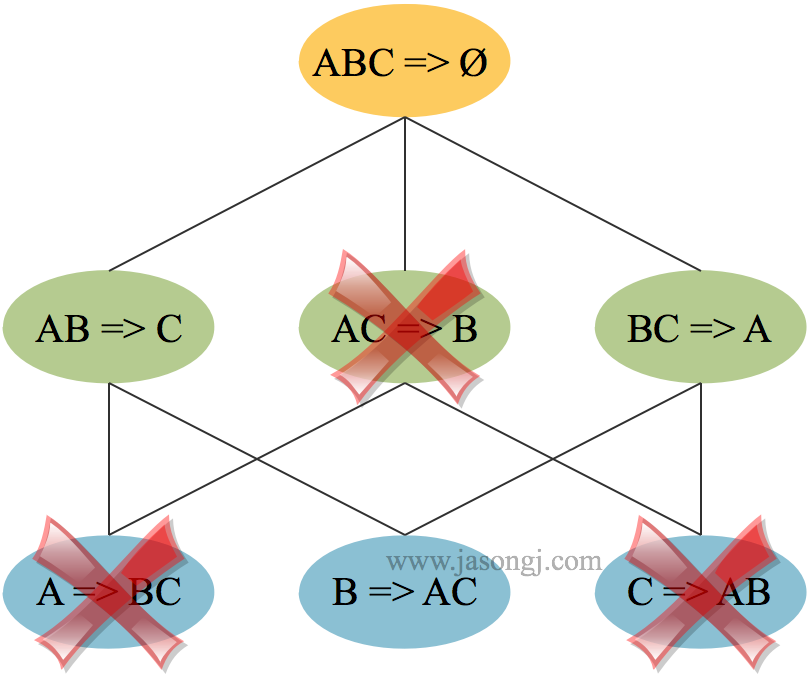
根据原理四，由 $1-$ 后件强关联规则，生成 $2-$ 后件关联规则 $\{B\} \rightarrow \{A，C\} $，置信度 $3/5 < 5/7$，不是强关联规则。

至此，本例中通过Apriori算法得到强关联规则 $\{A，B\} \rightarrow C $ 与 $\{B，C\} \rightarrow A $。

注：这里只演示了从 $3-$ 频繁项目集中挖掘强关联规则。实际上同样还可以从上文中得到的 $2-$ 频繁项目集中挖掘出更多强关联规则，这里不过多演示。

总结

Aprior原理和实现简单，相对穷举法有其优势，但也有其局限

从单元素项集开始，通过组合满足最小支持度要求的项集来形成更大的集合
通过上述四条原理，进行剪枝，降低了计算量，从而提升了计算速度
每次增加频繁项目集的大小，都需要重新扫描整个数据集（计算支持度）
当数据集很大时，频繁项目集的生成速度会显著降低
需要频繁扫描数据集从而从候选项目集中筛选出频繁项目集，开销较大

FP-growth算法

构建FP树

生成交易数据集
设有交易数据集如下

1：A，F，H，J，P
2：F，E，D，W，V，U，C，B
3：F
4：A，D，N，O，B
5：E，A，D，F，Q，C，P
6：E，F，D，E，Q，B，C，M

项目过滤及重排序
与Apriori算法一样，获取频繁项集的第一步是根据支持度阈值获取 $1-$ 频繁项目集。不一样的是，FP-growth 算法在获取 $1-$ 频繁项目集的同时，对每条交易只保留 $1-$ 频繁项目集内的项目，并按其支持度倒排序。

这里将最小支持度设置为 $3/6$。第一遍扫描数据集后得到过滤与排序后的数据集如下：

1：F，A
2：F，D，E，B，C
3：F
4：D，B，A
5：F，D，E，A，C
6：F，D，E，B，C

构建FP树
TP-growth算法将数据存储于一种称为 FP 树的紧凑数据结构中。FP 代表频繁模式（Frequent Pattern）。FP 树与其它树结构类似，但它通过链接（link）来连接相似元素，被连接起来的项目可看成是一个链表。

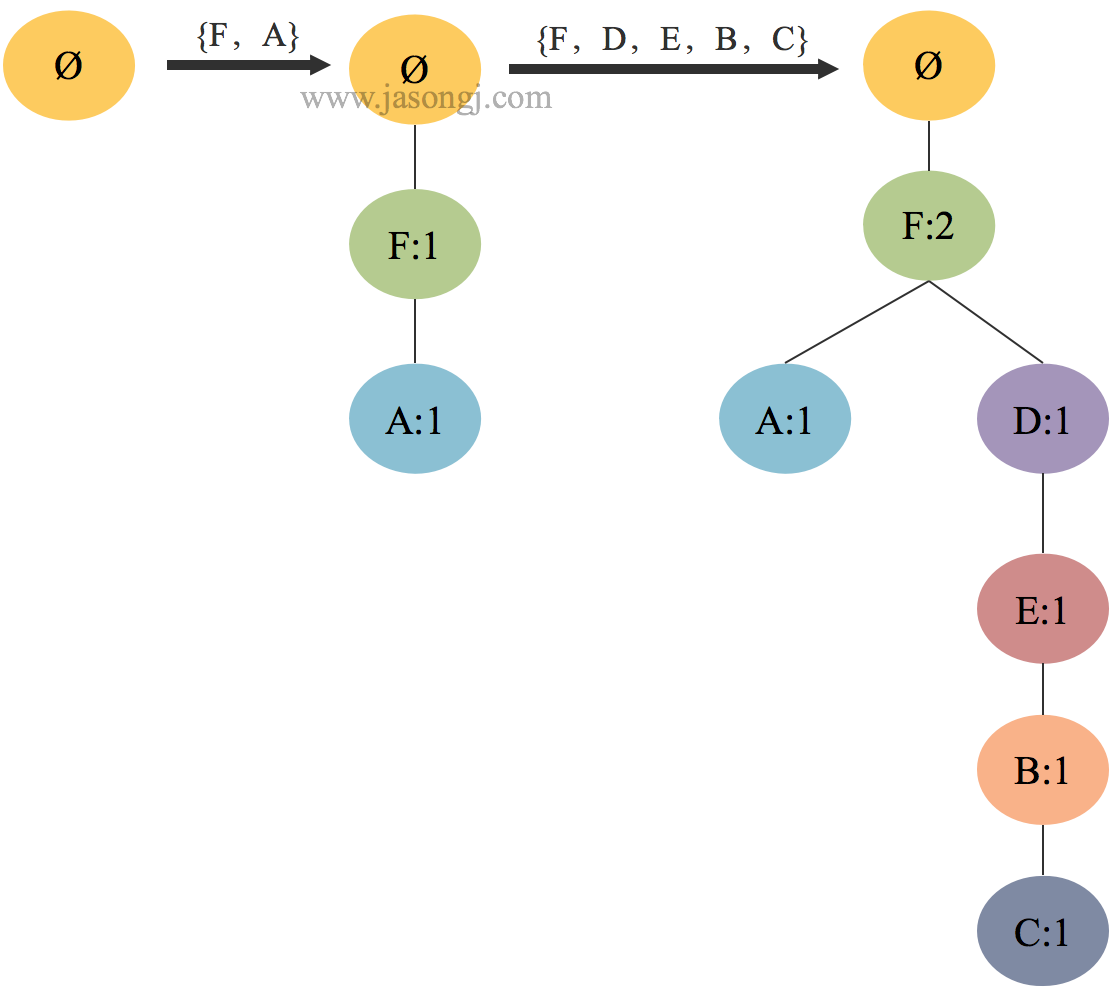
FP树的构建过程是以空集作为树的根节点，将过滤和重排序后的数据集逐条添加到树中：如果树中已存在当前元素，则增加待添加元素的值；如果待添加元素不存在，则给树增加一个分支。

添加第一条记录时，直接在根节点下依次添加节点 $ \lt F：1 \gt $， $ \lt A：1 \gt $ 即可。添加第二条记录时，因为 $\{F，D，E，B，C\}$ 与路径 $\{F:1，A:1\}$ 有相同前缀 $F$ ，因此将 $F$ 次数加一，然后在节点 $ \lt F：2 \gt $ 下依次添加节点 $ \lt D：1 \gt $， $ \lt E：1 \gt $， $ \lt B：1 \gt $， $ \lt C：1 \gt $。

第一条记录与第二条记录的添加过程如下图所示。

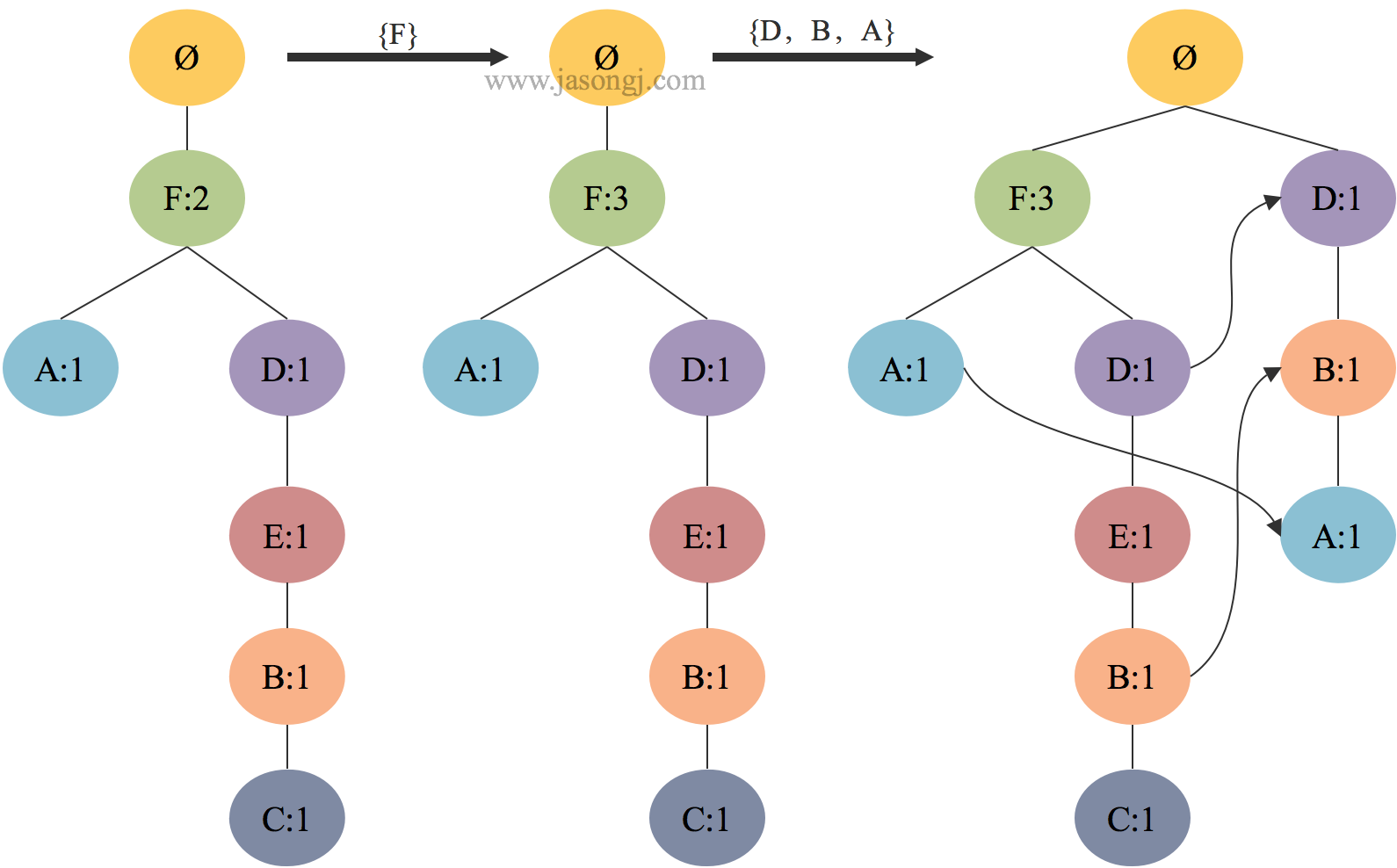
添加第三条记录 $\{F\}$ 时，由于 $FP$ 树中已经存在该节点且该节点为根节点的直接子节点，直接将 $F$ 的次数加一即可。

添加第四条记录 $\{D，B，A\}$ 时，由于与 $FP$ 树无共同前缀，因此直接在根节点下依次添加节点 $ \lt D：1 \gt $， $ \lt B：1 \gt $， $ \lt A：1 \gt $。

第三条记录与第四条记录添加过程如下所示

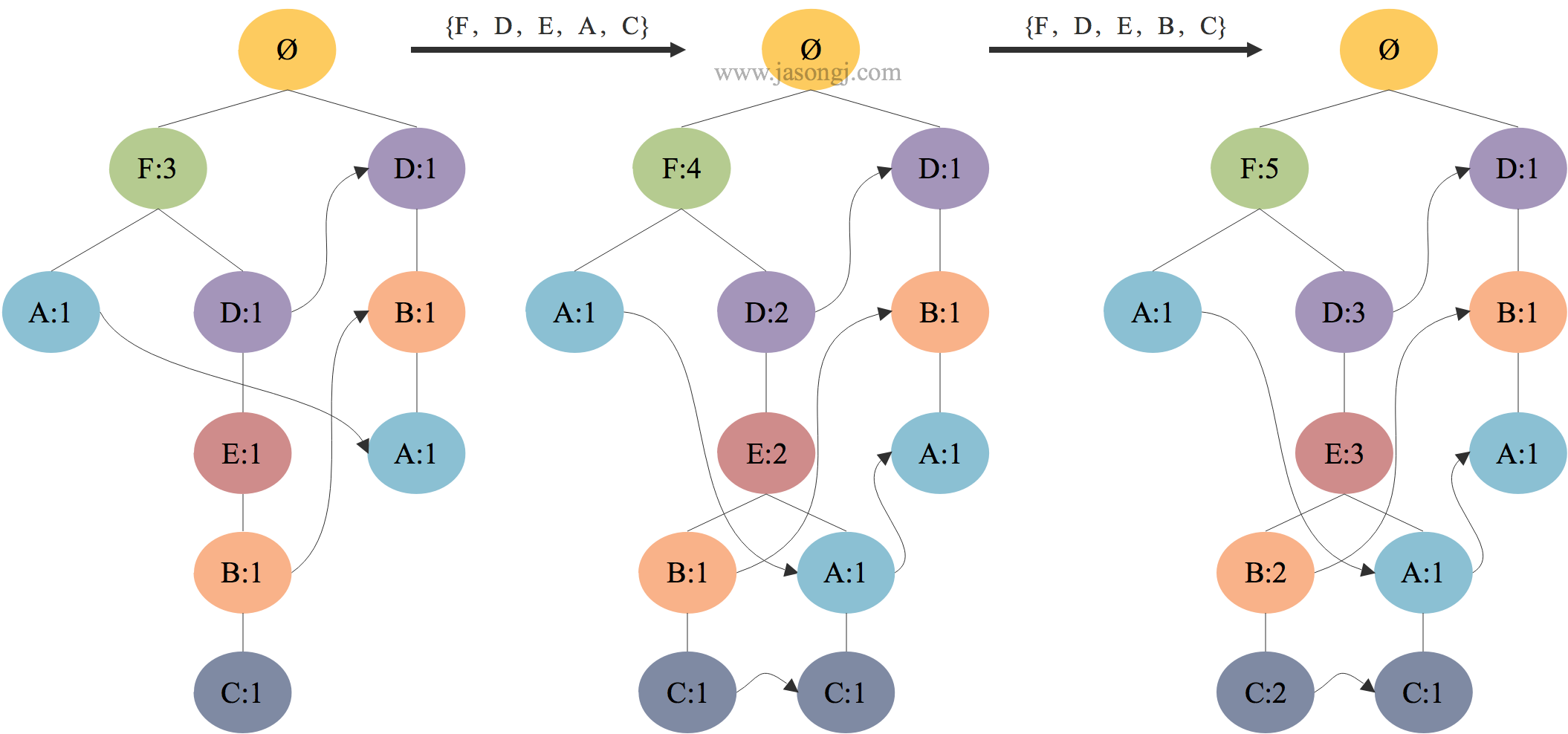
添加第五条记录 $\{F，D，E，A，C\}$ 时，由于与 $FP$ 树存在共同前缀 $\{F，D，E\}$ 。因此先将其次数分别加一，然后在节点 $ \lt E：1 \gt $ 下依次添加节点 $ \lt A：1 \gt $， $ \lt C：1 \gt $。

添加第六条记录 $\{F，D，E，B，C\}$ 时，由于 $FP$ 树已存在 $\{F，D，E，B，C\}$ ，因此直接将其次数分别加一即可。

第五条记录与第六条记录添加过程如下图所示。

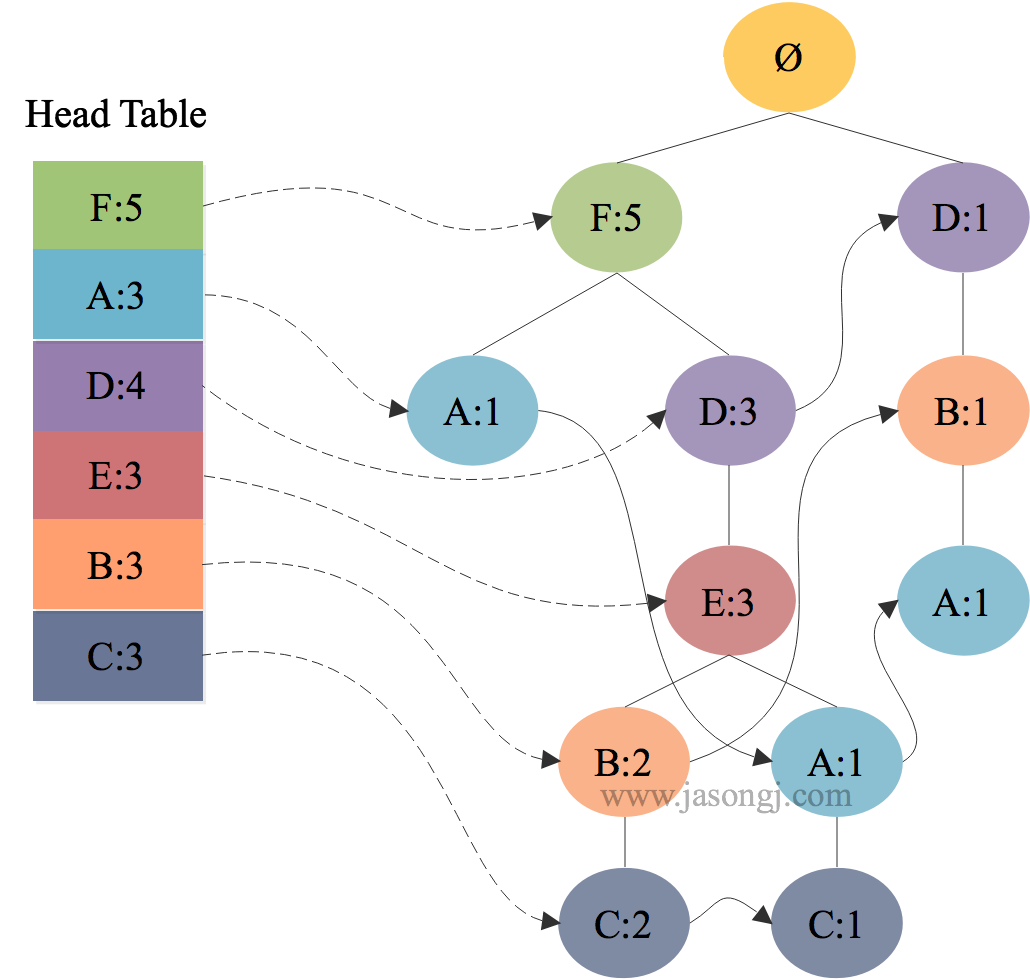
建立头表
为了便于对整棵FP树进行遍历，可建立一张项目头表。这张表记录各 $1-$ 频繁项的出现次数，并指向该频繁项在 $FP$ 树中的节点，如下图所示。

从FP树中挖掘频繁项目集

构建好 $FP$ 树后，即可抽取频繁项目集，其思路与 Apriori 算法类似——先从 $1-$ 频繁项目集开始，然后逐步构建更大的频繁项目集。

从 $FP$ 树中抽取频繁项目集的三个基本步骤如下：

从 $FP$ 树中获得条件模式基（conditional pattern base）
根据条件模式基构建 $条件FP树$
重复 $步骤1$ 与 $步骤2$ ，直到$ 条件FP树$ 只包含一个项目为止

抽取条件模式基
条件模式基（conditaional pattern base）是以所查元素为结尾的路径集合。这里的每一个路径称为一条前缀路径（prefix path）。前缀路径是介于所查元素与 $FP$ 树根节点间的所有元素。

每个 $1-$ 频繁项目的条件模式基如下所示

$1-$ 频繁项目	条件模式基
F	Ø：5
A	$\{D，B\}：1$，$\{F，D，E\}：1$，$\{F\}:1$
D	$\{F\}：3$，Ø：1
E	$\{F，D\}:3$
B	$\{F，D，E\}:2$，$\{D\}：1$
C	$\{F，D，E，B\}：2$，$\{F，D，E，A\}:1$

构建条件$FP$树
对于每个频繁项目，可以条件模式基作为输入数据构建一棵 $条件FP树$ 。

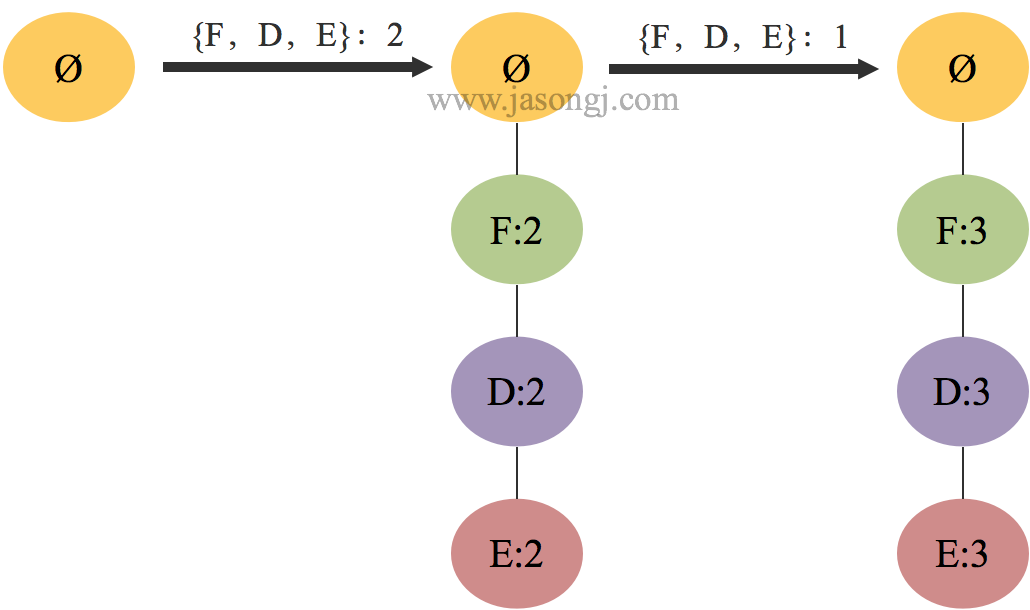
对于 $C$ ，其条件模式基为 $\{F，D，E，B\}：2$，$\{F，D，E，A\}:1$ 。根据支持度阈值 $3/6$ 可排除掉 $A$ 与 $B$ 。以满足最小支持度的 $\{F，D，E\}：2$ 与 $\{F，D，E\}:1$ 构建 $条件FP树$ 如下图所示。

递归查找频繁项集
基于上述步骤中生成的 $FP树$ 和 $条件FP树$ ，可通过递归查找频繁项目集。具体过程如下：

1 初始化一个空列表 $prefix$ 以表示前缀
2 初始化一个空列表 $freqList$ 存储查询到的所有频繁项目集
3 对 $Head Table$ 中的每个元素 $ele$，递归：
　　3.1 记 $ele + prefix$ 为当前频繁项目集 $newFreqSet$
　　3.2 将 $newFreq$ 添加到 $freqList$中
　　3.3 生成 $ele$ 的 $条件FP树$ 及对应的 $Head Table$
　　3.4 当 $条件FP树$ 为空时，退出
　　3.5 以 $条件FP树$ 树与对应的 $Head Table$ 为输入递归该过程

对于 $C$ ，递归生成频繁项目集的过程如下图所示。

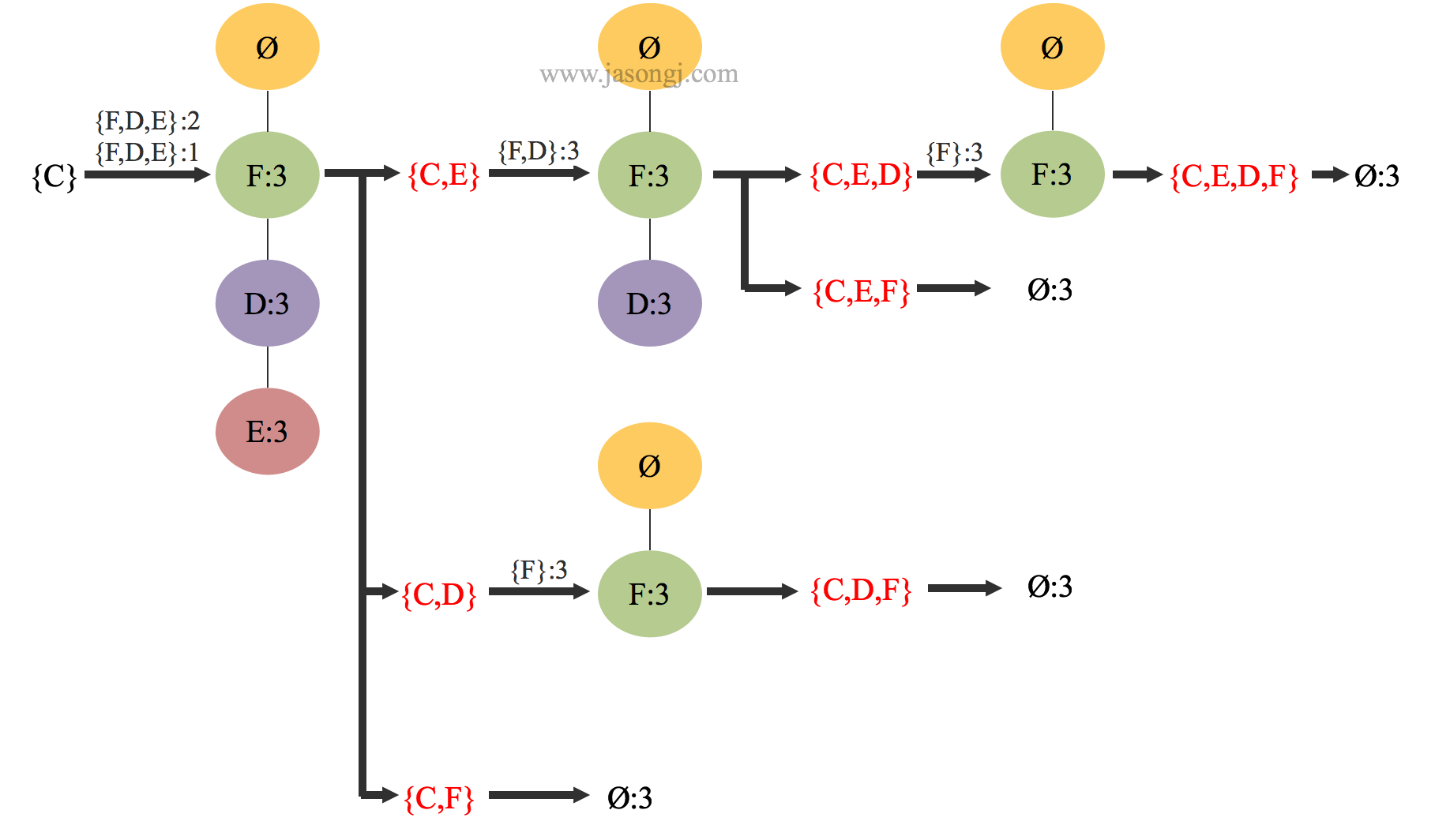
Conditaional Frequent Pattern Tree for C

上图中红色部分即为频繁项目集。同理可得其它频繁项目集。

生成强关联规则

得到频繁项目集后，即可以上述同样方式得到强关联规则。

总结

$FP-growth$ 算法相对 $Apriori$ 有优化之处，但也有其不足

无论数据集多复杂，只需扫描原始数据集两遍，速度比 $Apriori$ 算法快
实现比 $Apriori$ 算法复杂

Apriori算法R语言实战

加载数据集

$R$ 语言中，$arules$ 包提供了 $Apriori$ 算法的实现。

1	library(arules)

将上文Apriori生成频繁项目集中的数据集存于 $transaction.csv$ 文件。然后使用 $arules$ 包的 $read.transactions$ 方法加载数据集并存于名为 $transactions$ 的稀疏矩阵中，如下

1	transactions <- read.transactions("transaction.csv", format="basket", sep=",")

这里之所以不使用 $data.frame$ 是因为当项目种类太多时 $data.frame$ 中会有大量单元格为 $0$，大量浪费内存。稀疏矩阵只存 $1$，节省内存。

该方法的使用说明如下

Usage:
read.transactions(file, format = c("basket", "single"), sep = "",
                  cols = NULL, rm.duplicates = FALSE, 
                  quote = "\"'", skip = 0, 
                  encoding = "unknown")

其中，$format=”basket”$ 适用于每一行代表一条交易记录（ $basket$ 可理解为一个购物篮）的数据集，本例所用数据集即为该类型。$format=”single”$ 适用于每一行只包含一个事务 $ID$ 和一件商品（即一个项目）的数据集，如下所示。

1，A
1，B
1，C
2，B
2，D
3，A

$rm.duplicates=TRUE$ 代表删除同一交易（记录）内的重复商品（项目）。本例所用数据集中每条记录无重复项目，故无须设置该参数。

分析数据

查看数据集信息

> inspect(transactions)
    items    
[1] {A,B,C}  
[2] {A,B,D}  
[3] {A,C,D}  
[4] {A,B,C,E}
[5] {A,C,E}  
[6] {B,D,E}  
[7] {A,B,C,D}

查看数据集统计信息

> summary(transactions)

transactions as itemMatrix in sparse format with
 7 rows (elements/itemsets/transactions) and
 5 columns (items) and a density of 0.6571429 

most frequent items:
      A       B       C       D       E (Other) 
      6       5       5       4       3       0 

element (itemset/transaction) length distribution:
sizes
3 4 
5 2 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  3.000   3.000   3.000   3.286   3.500   4.000 

includes extended item information - examples:
  labels
1      A
2      B
3      C

从中可看出，总共包含 $7$ 条交易，$5$ 种不同商品。同时可得到出现频次最高的 $5$ 个项目及其频次。另外，所有事务中包含 $3$ 件商品的有 $5$ 个，包含 $4$ 件商品的有 $2$ 个。

接下来，可通过 $itemFrequency$ 方法查看各项目的支持度，如下所示。

1
2
3

> sort(itemFrequency(transactions), decreasing = T)
        A         B         C         D         E 
0.8571429 0.7142857 0.7142857 0.5714286 0.4285714

挖掘关联规则

上面对数据的观察，其目的是找出合适的支持度阈值与置信度阈值。这里继续使用 $3/7$ 作为最小支持度， $5/7$ 作为最小置信度。

1	rules <- apriori(transactions, parameter = list(support = 3/7, confidence = 5/7, minlen = 2))

其中 $minlen = 2$ 是指规则至少包含两个项目，即最少一个前件一个后件，如 $\{A\} \rightarrow B $。结果如下

> inspect(rules)
    lhs      rhs support   confidence lift     
[1] {D}   => {B} 0.4285714 0.7500000  1.0500000
[2] {D}   => {A} 0.4285714 0.7500000  0.8750000
[3] {B}   => {A} 0.5714286 0.8000000  0.9333333
[4] {C}   => {A} 0.7142857 1.0000000  1.1666667
[5] {A}   => {C} 0.7142857 0.8333333  1.1666667
[6] {B,C} => {A} 0.4285714 1.0000000  1.1666667
[7] {A,B} => {C} 0.4285714 0.7500000  1.0500000

从中可以看出，$Apriori$ 算法以 $3/7$ 为最小支持度，以 $5/7$ 为最小置信度，从本例中总共挖掘出了 $7$ 条强关联规则。其中 $2$ 条包含 $3$ 个项目，分别为 $\{B，C\} \rightarrow A $ 与 $\{A，B\} \rightarrow C $。该结果与上文中使用 $Apriori$ 算法推算出的结果一致。

评估关联规则

挖掘出的强关联规则，不一定都有效。因此需要一些方法来评估这些规则的有效性。

提升度
第一种方法是使用上文中所述的提升度来度量。本例中通过 $Apriori$ 算法找出的强关联规则的提升度都小于 $3$，可认为都不是有效规则。

> inspect(sort(rules, by = "lift"))
    lhs      rhs support   confidence lift     
[1] {C}   => {A} 0.7142857 1.0000000  1.1666667
[2] {A}   => {C} 0.7142857 0.8333333  1.1666667
[3] {B,C} => {A} 0.4285714 1.0000000  1.1666667
[4] {D}   => {B} 0.4285714 0.7500000  1.0500000
[5] {A,B} => {C} 0.4285714 0.7500000  1.0500000
[6] {B}   => {A} 0.5714286 0.8000000  0.9333333
[7] {D}   => {A} 0.4285714 0.7500000  0.8750000

其它度量
$interestMeasure$ 方法提供了几十个维度的对规则的度量

> interestMeasure(rules, c("coverage","fishersExactTest","conviction", "chiSquared"), transactions=transactions)
   coverage fishersExactTest conviction chiSquared
1 0.5714286        0.7142857  1.1428571 0.05833333
2 0.5714286        1.0000000  0.5714286 0.87500000
3 0.7142857        1.0000000  0.7142857 0.46666667
4 0.7142857        0.2857143         NA 2.91666667
5 0.8571429        0.2857143  1.7142857 2.91666667
6 0.4285714        0.5714286         NA 0.87500000
7 0.5714286        0.7142857  1.1428571 0.05833333

> rule_measures <- interestMeasure(rules, c("coverage","fishersExactTest","conviction", "chiSquared"), transactions=transactions)  
> quality(rules) <- cbind(quality(rules), rule_measures)
> inspect(sort(rules, by = "fishersExactTest", decreasing = T))

    lhs      rhs coverage  fishersExactTest conviction chiSquared coverage  fishersExactTest conviction chiSquared
[1] {D}   => {A} 0.5714286 1.0000000        0.5714286  0.87500000 0.5714286 1.0000000        0.5714286  0.87500000
[2] {B}   => {A} 0.7142857 1.0000000        0.7142857  0.46666667 0.7142857 1.0000000        0.7142857  0.46666667
[3] {D}   => {B} 0.5714286 0.7142857        1.1428571  0.05833333 0.5714286 0.7142857        1.1428571  0.05833333
[4] {A,B} => {C} 0.5714286 0.7142857        1.1428571  0.05833333 0.5714286 0.7142857        1.1428571  0.05833333
[5] {B,C} => {A} 0.4285714 0.5714286               NA  0.87500000 0.4285714 0.5714286               NA  0.87500000
[6] {C}   => {A} 0.7142857 0.2857143               NA  2.91666667 0.7142857 0.2857143               NA  2.91666667
[7] {A}   => {C} 0.8571429 0.2857143        1.7142857  2.91666667 0.8571429 0.2857143        1.7142857  2.91666667

总结

关联规则可用于发现项目间的共生关系
支持度与置信度阈值可筛选出强关联规则

分享交流大数据领域技术，包括但不限于Storm、Spark、Hadoop等流行分布式计算系统，Kafka、MetaQ等分布式消息系统，MongoDB、Cassandra等NoSQL，PostgreSQL、MySQL等RDBMS以及其它前沿技术

机器学习（三）关联规则R语言实战 Apriori

关联规则背景

关联规则来源

什么是关联规则

关联规则的核心概念

Apriori算法

Apriori算法原理

Apriori生成频繁项集

生成强关联规则

总结

FP-growth算法

构建FP树

从FP树中挖掘频繁项目集

生成强关联规则

总结

Apriori算法R语言实战

加载数据集

分析数据

挖掘关联规则

评估关联规则

总结

《机器学习》系列文章